Ist die Erde eine Kugel?

[Konrad Juckreiz]

Meine Herren,

Es gab noch nie einen Menschen, der die Rückseite der Erdscheibe gesehen hat.

Oh, da gab es schon viele. Die meisten davon allerdings nicht freiwillig.

Tatsächlich wurde die Hölle bereits von Herrn Juckreiz in der Scheibenwelt lokalisiert, nicht darunter. Diese Frage ist also noch offen.

Dies ist zwar noch Gegenstand der aktuellen Forschung, wurde aber schon in diesem Beitrag differenzierend betrachtet.

Froh, sich auf der Oberseite der Oberfläche zu befinden,
______________________________________________

[Martin Berger]

Auf eine Antwort des Erdumrundungsproblem hoffend

Knabbub Rosengarten,

gestehen Sie endlich, daß Sie diesen Faden bestenfalls überflogen haben. Das Thema Weltumrundung war vor noch gar nicht allzu langer Zeit ein Thema. Wenn Sie darüber nichts gelesen haben, haben Sie sich den Faden nicht durchgelesen. In diesem Fall können Sie lange auf eine Antwort warten.

Erbost,
Martin Berger

[Prof Dr Rosengarten]

Herr Juckreiz,

Falls es schon Menschen gab, die die Rückseite sahen, warum finde ich nirgendwo Berichte oder Beweise (sowohl bei Suchmaschine (unredl.) Google als auch in sämtlicher Literatur, die mir verfügbar ist? Warum waren diese Menschen unfreiwillige Betrachter eines nach meinen Vorstellungen besonderen Rundblickes? Könnten Sie mir eventuell Menschen (eine Verschaltung wäre sehr nett, falls es Internetzseiten zu diesem Thema gibt), die die Möglichkeit eines Blickes auf die Rückseite hatten, nennen? Ich persönlich bin der Meinung, dass die Hölle nicht unterhalb der Erde liegt, denn in diesem Falle befände sich die Menschheit ja nur wenige Kilometer vom Höllenfeuer und dem Mephistopheles selbst getrennt. Der negative Einfluss würde redliche Christen wie Sie in den Wahnsinn treiben.

Herr Berger,

Wie ich schon erwähnte habe ich den Faden mit der Lupe untersucht, dabei aber keine wissenschaftlich dokumentierbaren Erkenntnisse beaugapfeln können. Falls Sie anderer Meinung und im besten Falle auch eine Verschaltung parat haben entschuldige ich mich für mein langsam arbeitendes Denkorgan, ich bin eben nicht mehr der Jüngste.

Seine Meinung vertretend,
Rosengarten

[Konrad Juckreiz]

Schwachkopf Rosengürtel,

Falls es schon Menschen gab, die die Rückseite sahen, warum finde ich nirgendwo Berichte oder Beweise (sowohl bei Suchmaschine (unredl.) Google als auch in sämtlicher Literatur, die mir verfügbar ist?

Was die Ihnen verfügbare Literatur angeht glaube ich Ihnen auf's Wort, aber bei Gockel findet man eine große Menge von Informationen. Wie dem auch sei, ein Bild sagt mehr als 1000 Worte:

Warum waren diese Menschen unfreiwillige Betrachter eines nach meinen Vorstellungen besonderen Rundblickes?

Siehe oben.

Könnten Sie mir eventuell Menschen (eine Verschaltung wäre sehr nett, falls es Internetzseiten zu diesem Thema gibt), die die Möglichkeit eines Blickes auf die Rückseite hatten, nennen?

In diesem Beitrag gibt es dazu eine Schaltung.

Ich persönlich bin der Meinung, dass die Hölle nicht unterhalb der Erde liegt, denn in diesem Falle befände sich die Menschheit ja nur wenige Kilometer vom Höllenfeuer und dem Mephistopheles selbst getrennt. Der negative Einfluss würde redliche Christen wie Sie in den Wahnsinn treiben.

Ihre persönliche Meinung zeugt höchstens von Ihrer eigenen Idiotie.

Wie ich schon erwähnte habe ich den Faden mit der Lupe untersucht, dabei aber keine wissenschaftlich dokumentierbaren Erkenntnisse beaugapfeln können. Falls Sie anderer Meinung und im besten Falle auch eine Verschaltung parat haben entschuldige ich mich für mein langsam arbeitendes Denkorgan, ich bin eben nicht mehr der Jüngste.

Wurde bereits hier behandelt.

Seine Meinung vertretend, Rosengarten

Ihre Dummheit breittretend würde es wohl besser treffen.

Ohrfeigend,
_________

[Prof Dr Rosengarten]

Werter Herr Reizjuck (Sie wollen meinen Benutzernamen nicht richtig schreiben? Ich ebenfalls nicht)!

Wie ich sehe haben Sie das Buch von Thomas L. Friedmann (der übrigens ein Kolumnist ist) nicht gelesen, sonst würden Sie den Inhalt kennen. Das Bild auf dem Buchumschlag sagt in diesem Fall kein einziges Wort aus. Das Buch ist weltpolitisch - kritisch geschrieben und enthält zehn Faktoren, die die Welt metaphorisch als flach beschreiben:
Faktor 1: Der 9. November 1989. Als die Mauern fielen und Windows die Fenster zur Welt öffnete
Faktor 2: Der 9. August 1995. Das neue Zeitalter der Konnektivität: Als das Web über die Welt gespannt wurde und Netscape an die Börse ging
Faktor 3: Workflow-Software und die digitale Organisation des Arbeitsablaufs. Lass uns essen gehen – unsere Computer machen einen Termin
Faktor 4: Das Hochladen. Wie man sich die Kompetenzen von Gemeinschaften nutzbar machen kann
Faktor 5: Outsourcing. Das Jahr-2000-Problem
Faktor 6: Offshoring. Mit den Gazellen rennen, mit den Löwen fressen
Faktor 7: Globale Wertschöpfungsketten. Sushi in Arkansas
Faktor 8: Insourcing. Was die Jungs in den komischen braunen Hemden wirklich tun
Faktor 9: Selbstinformation. Google, Yahoo!, MSN Web Search
Faktor 10: Die Steroide. Digital, mobil, persönlich und virtuell
Ich rate Ihnen, bevor Sie Behauptungen aufzustellen wie Ihre obige, zuerst betroffene Literatur zu lesen.
Meine eigene Meinung zeugt keineswegs von Idiotie, sie zeugt von der Gabe des selbstständigen Denkens.

Recht habend,
Rosengarten

[Konrad Juckreiz]

Dosenfleischer Herpesvirus,

was müllen Sie hier das Brett mit einem Inhaltsverzeichnis, welches im Gegensatz zum Umschlagsbild mit dem Fadenthema nichts zu tun hat, zu ? Alleine für die vielen Anglizismen gehören Sie schon bestraft.

Belästigt,
_______

[Prof Dr Rosengarten]

Herr Juckreiz!

Ihr Beitrag hat mit dem Fadenthema nicht das Geringste zu tun, da Sie hier weltpolitische Literatur von Kolumnisten als den Beweis der Erde in Scheibenform darstellen.
Ein Inhaltsverzeichnis habe ich ebenfalls nicht geschrieben, lediglich die zehn Faktoren, die das Buch beinhaltet (für die vielen Anglizismen entschuldige ich mich), da Sie es nicht gelesen haben!
Ich bin weder ein Dosenfleischer noch ein Herpesvirus! Fällt Ihnen nichts besseres ein als mich zu beleidigen?

Empört zu Bett gehend,
Rosengarten

[Konrad Juckreiz]

Depp Mimosengarten,

Ich bin weder ein Dosenfleischer noch ein Herpesvirus! Fällt Ihnen nichts besseres ein als mich zu beleidigen?

Bloß weil Sie es abstreiten, heisst das noch lange nicht, daß Sie es nicht sind. Wenn ich mir Ihre bisherigen Vandalenakte hier so ansehe, kann ich nur zum Schluß kommen, daß Sie es sehr wohl sind.

Ihr Beitrag hat mit dem Fadenthema nicht das Geringste zu tun, da Sie hier weltpolitische Literatur von Kolumnisten als den Beweis der Erde in Scheibenform darstellen.

Als Beweis für Ihre Dummheit, Herr Rosenbartel, nicht für die Scheibenform der Erde. Diese wurde bereits in den Beiträgen, die Sie sich vehement zu lesen weigern, bewiesen.

◈

Rechengenie Faber.

Und außerdem, wenn Sie annehmen, dass die Luft sich so verteilt, weil von der Erde ein radialsymmetrisches Gravitationsfeld ausgeht, habe ich dazu später noch einiges zu sagen.

So wie Sie sich bisher mit Formeln angestellt haben, wage ich es ja zu bezweifeln, daß Sie über ein idealisiertes g=G·M/r² bei einem infinitesmal kleinem Gravitationszentrum hinauskommen werden. In der Tat müssen Sie dabei aber mindestens die modifizierte Neutonnendynamik anwenden, für g den Wert g=√(G·M·a₀)/r setzen und in die Formel für g'=(g/a₀)/√[1+(g/a₀)²]*g einsetzen. Die Variable a₀ hat die Einheit einer Beschleunigung und kann jeden Wert zwischen 1 und cosh(g/x)*g annehmen. Das genaue Verhalten des x-Parameters ist jedoch noch Gegenstand aktueller Forschung, was die Sache ein wenig verkompliziert. Nichtsdestotrotz, sollten Sie so weit kommen, müssen Sie als nächstes nach infinitesmal kleinen Teilstücken und deren Feldlinien, auch hier je mehr desto besser, integrieren. Hier eine grobe Skizze mit drei Teilstücken [0:0, 4:0, 8:0] in zwei Dimensionen:



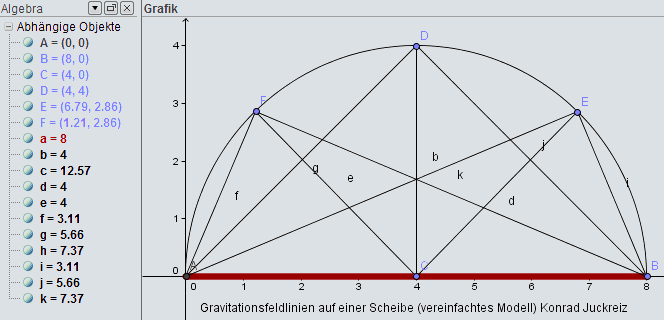
x-Achse: Breite, y-Achse: Höhe. Erde: rot markiert.


Die Kleinbuchstaben stehen im Bild als Variablen für die Distanz zum gravitativ wirkenden Teilstück der Erde, in der obigen Formel mit r bezeichnet. Sie müssen die Prozedur also für g'(ra), g'(rb), g'(rc), usw ausführen - nach je kleineren (und damit mehr) Teilstücken Sie die Integration durchführen, desto genauer wird dann Ihr Ergebnis (aber auch aufwändiger).

Danach müssen Sie eine dritte Dimension hinzufügen und die Teilstücke mit dem Abstand zum Zentrum mal 2 Pi multiplizieren. Dann erhalten Sie eine relativ gleichmässige Fallbeschleunigung am Boden, während bei großen Höhen ein kuppelförmiges Feld entsteht, wonach das Magnetfeld der Erde noch für den letzten Feinschliff sorgt und die Iono- und Exosphäre glättet.

Seit nunmehr zwei Jahren den Heimrechner an einer solchen Simulation mit einer Auflösung von 6e24*1kg zu 7.7e22 Amperequadratmetern rechnen lassend und das endgültige Ergebnis in einem weiteren Jahr erwartend,

[Haxntoni]

geehrte Herren,

Heut hab ich es geschafft diesen von Pharisäern und Spekulanten überfluteten Brettabschnitt zu lesen. Es war wirklich schlimm.
Wären hier nicht auch so ausgefuchste Menschen wie der Herr Berger, Herr Juckreiz oder der unnachahmliche Herr Korschio wäre es wirklich ein einziges Trauerspiel. So präzise Bombenfeste Argumentation und Veranschaulichung sind mir selten untergekommen.
Meinen ergebensten Dank hierfür. Mir drängt sich die Annahme auf das sie alle sehr bayerische Lehrer gehabt haben müssen.

Herr Juckreiz,
ich gestehe zu meiner Schande dass ich von alldem was sie hier so wunderbar wiedergeben vorher keine Ahnung hatte.
Ich wusste lediglich das Gott es so wollte wie es ist. Zudem war mir auch klar dass er, solange wir z.B. genug beten oder dafür sorgen das Frauen nichts zu melden haben, es auch nicht ändern wird. Aber um die komplexen Zusammenhänge zu verstehen, war es nicht von Belang so alt zu werden wie ich es bin oder die tägliche Zeitung zu lesen, nein. Dafür hätte es gereicht ihre ca. 30 Beiträge in disem Abschnitt zu lesen.
Ich hoffe innigst, dass mir dieses lange währende Unwissen beim Jüngsten Gericht nicht einmal negativ angerechnet wird.

Und als ob die Überzeugungskraft dieser Herren noch nicht genug wäre findet sich immer wieder ein hinterfotziger Neunmalklug und wiederholt all das widerlegte Gechwätz der ersten Seiten. Es gibt halt einfach zuviele von diesen fehlgeleiteten Wahnsinnigen und da ihnen ja schon längst keine neuen Argumente mehr einfallen, klauben sie einfach die alten wieder auf.
So langsam jedoch scheint sich Verzweiflung und Panik in den luftbefüllten Gehirnen dieser Physikterroristen breit zu machen. Das erkennt man sehr gut an dem wirren geschreibsel eines Herrn Rosengarten.

Diese Niederringung von unchristlichen Theorien hat mich zutiefst berührt.


gerührt,

Haxntoni

[Lancelotta]

Herr Toni!
Endlich konnte ich einmal meinen Brecheimer beiseite stellen.
Nur an der Rechtschreibung müssen Sie noch feilen.

Ein Hoch auf unser schönes Bayern ausrufend
Lancelotta
Erste Hüterin der Heiligen Handgranate

[johnfaber]

Herr Juckreiz,
Es ist erstaunlich, dass Sie Newton'sche Gravitationsgesetze voraussetzen, wenn Sie die Erde für eine Scheibe halten. Ich sehe da nämlich keinen Grund, warum der Mittelpunkt dann nicht unter dem Gewicht der Randgebiete zusammenstürzen sollte.
Außerdem beschreibt Wikipedia die modifizierte Newtonsche Mechanik als Erklärungsansatz, um das Bewegungsverhalten großer Galaxien zu erklären- welche im Scheibenmodell nicht existieren! Denn die Sterne sind ja laut Ihnen an die Himmelskuppel angebracht, wo sie schwerlich solche komplexen Systeme wie eine Galaxie hervorbringen können.
Ihr
John Faber
PS: Wieder zwei Dosenfleischer, die so tun, als würden sie der Administranz zustimmen. Die haben alle solche Erkenungsmerkmale.

[Lancelotta]

Herr Juckreiz,
Es ist erstaunlich, dass Sie Newton'sche Gravitationsgesetze... bla.... Klugfäkaliererei....
PS: Wieder zwei Dosenfleischer, die so tun, als würden sie der Administranz zustimmen. Die haben alle solche Erkenungsmerkmale.

So viel Weisheit ist nicht gut für Sie.

Dem Purschen die Löffel wegnehmend

Lancelotta
Erste Hüterin der Heiligen Handgranate

[Konrad Juckreiz]

Dosenfleischer Faber.

Es ist erstaunlich, dass Sie Newton'sche Gravitationsgesetze voraussetzen, wenn Sie die Erde für eine Scheibe halten.

Gerade habe ich Ihnen doch erklärt, warum die neutonnischen Formeln dazu nicht ausreichen. Ich arbeite mit den milgrom'schen Gravitationsgesetz, wo im Gegensatz zu Ihrem veralteten Modell der göttliche Wille über die x Variable einfliesst, während das göttliche Gesetz in G und r sowie der göttliche Wille in der M Variable ausgedrückt wird.

Ich sehe da nämlich keinen Grund, warum der Mittelpunkt dann nicht unter dem Gewicht der Randgebiete zusammenstürzen sollte.

Sie können ja auch weder rechnen noch lesen.

Außerdem beschreibt Wikipedia die modifizierte Newtonsche Mechanik als Erklärungsansatz, um das Bewegungsverhalten großer Galaxien zu erklären.

Das hängt alles vom μ ab. Ihnen empfehle ich jedoch, sich mit den normalen Grundrechenarten auseinanderzusetzen, bevor Sie sich an solche Rechnungen wagen.

,

[johnfaber]

Herr Juckreiz,
Seit wann sind menschliche Gehirne in der Lage, den göttlichen Willen zu erfassen, geschweige denn in Variablen zu simplifizieren? Oder, wie hier bei Ihnen, in zweien?

[...]wo im Gegensatz zu Ihrem veralteten Modell der göttliche Wille über die x Variable einfliesst, während das göttliche Gesetz in G und r sowie der göttliche Wille in der M Variable ausgedrückt wird.

Wenn Sie tatsächlich glauben, Sie wüssten, was Gott will- falls das Wort "wollen" dafür überhaupt ausreicht- sind Sie nicht besser als jeder beliebige Ketzer.

[...]wonach das Magnetfeld der Erde noch für den letzten Feinschliff sorgt und die Iono- und Exosphäre glättet.

Das Magnetfeld hat Einflüsse auf die Atmosphäre? Wie das, ohne elektro- oder ferromagnetische Elemente? Ja, in der Ionosphäre sind Ionen, welche theoretisch vom Magnetfeld verschoben werden könnten, aber von "glätten" kann keinesfalls gesprochen werden. Nicht bei der Form, die das Erdmagnetfeld hat. Diese ist nämlich auf der Scheibenerde ebenso wie auf der Kugelerde geformt wie ein Torus, was bedeutet, dass die Atmosphäre nach diesem Modell am magnetischen Nordpol den Boden berühren müsste, odrr zumindest die Ionosphäre Dass dem nicht so ist, weiß man.
Ihr
John Faber

[Konrad Juckreiz]

Lügenautomat Faber.

Seit wann sind menschliche Gehirne in der Lage, den göttlichen Willen zu erfassen

Seit er in der Bibel geoffenbart wurde.

geschweige denn in Variablen zu simplifizieren? Oder, wie hier bei Ihnen, in zweien?

Gottes Wille findet sich in allen Variablen wieder, sofern diese die Realität beschreiben.

Wenn Sie tatsächlich glauben, Sie wüssten, was Gott will- falls das Wort "wollen" dafür überhaupt ausreicht- sind Sie nicht besser als jeder beliebige Ketzer.

Was Gott will, erfahren wir in der Bibel. Die Wissenschaft, sofern diese im Sinne der Bibel betrieben wird, bestätigt die Bibel:

Psalm 8,1-10: Seh ich den Himmel, das Werk deiner Finger, Mond und Sterne, die du befestigt: Was ist der Mensch, dass du an ihn denkst, des Menschen Kind, dass du dich seiner annimmst? Du hast ihn nur wenig geringer gemacht als Gott, hast ihn mit Herrlichkeit und Ehre gekrönt. Du hast ihn als Herrscher eingesetzt über das Werk deiner Hände, hast ihm alles zu Füßen gelegt.

Psalm 19,1-7: Die Himmel rühmen die Herrlichkeit Gottes, vom Werk seiner Hände kündet das Firmament. Ein Tag sagt es dem andern, eine Nacht tut es der andern kund, ohne Worte und ohne Reden, unhörbar bleibt ihre Stimme. Doch ihre Botschaft geht in die ganze Welt hinaus, ihre Kunde bis zu den Enden der Erde. Dort hat er der Sonne ein Zelt gebaut. Sie tritt aus ihrem Gemach hervor wie ein Bräutigam; sie frohlockt wie ein Held und läuft ihre Bahn. Am einen Ende des Himmels geht sie auf und läuft bis ans andere Ende; nichts kann sich vor ihrer Glut verbergen. Die Weisung des Herrn ist vollkommen, sie erquickt den Menschen. Das Gesetz des Herrn ist verlässlich, den Unwissenden macht es weise. Die Befehle des Herrn sind richtig, sie erfreuen das Herz; das Gebot des Herrn ist lauter, es erleuchtet die Augen.

Römerbrief 1,18-25: Der Zorn Gottes wird vom Himmel herab offenbart wider alle Gottlosigkeit und Ungerechtigkeit der Menschen, die die Wahrheit durch Ungerechtigkeit niederhalten. Denn was man von Gott erkennen kann, ist ihnen offenbar; Gott hat es ihnen offenbart. Seit Erschaffung der Welt wird seine unsichtbare Wirklichkeit an den Werken der Schöpfung mit der Vernunft wahrgenommen, seine ewige Macht und Gottheit. Daher sind sie unentschuldbar. Denn sie haben Gott erkannt, ihn aber nicht als Gott geehrt und ihm nicht gedankt. Sie verfielen in ihrem Denken der Nichtigkeit und ihr unverständiges Herz wurde verfinstert. Sie behaupteten, weise zu sein, und wurden zu Toren.

Mit dem letzten Satz sind auch Sie Narr gemeint !

was bedeutet, dass die Atmosphäre nach diesem Modell am magnetischen Nordpol den Boden berühren müsste

Natürlich berührt die Atmosphäre auch am Nordpol den Boden, oder meinen Sie etwa, dort herrscht ein Vakuum ?

Ihnen die Deppenkrone aufsetzend,
_____________________________